В № 11 нашего журнала за 1975 год в разделе «Панорама» была опубликована небольшая заметка «Математическая теория катастроф», в которой рассказывалось о работах известного французского математика Рене Тома, оказавшихся в центре внимания на нескольких международных математических конгрессах последних лет. Заметка заинтересовала многих наших читателей, которые в своих письмах просят рассказать более подробно о новой математической дисциплине.

        Более ста лет назад, работая над «Диалектикой природы», Фридрих Энгельс, отмечая крайне неравномерную математизацию различных наук, писал: «Применение математики: в механике твердых тел абсолютное, в механике газов приблизительное, в механике жидкостей уже труднее, в физике больше в виде попыток...; в химии простейшие уравнения первой степени; в биологии = 0». Причины этой неравномерности, пожалуй, наиболее ясно изложил современник Энгельса, русский математик Н.Бугаев. Он считал, что подобно тому, как природа являет собою мир непрерывных и прерывных величин, так и математика должна состоять из теории непрерывных функций – математического анализа – и теории прерывных функций – аритмологии. «Все приводит к мысли, - писал Бугаев, - что аритмология не уступит анализу по обширности своего материала, по общности своих приемов, по замечательной красоте своих результатов. Прерывность гораздо разнообразнее непрерывности. Можно даже сказать, что непрерывность есть прерывность, в которой изменение идет через бесконечно малые и равные промежутки».
        Сферой приложения аритмологических законов Бугаев считал строение химических элементов, протекание химических реакций, структуру химических соединений, строение кристаллов, биологические процессы. «Непрерывность объясняет только часть мировых событий, - писал Бугаев. – С непрерывностью непосредственно связаны аналитические функции. Эти функции приложимы к объяснению только простейших случаев жизни и природы».
    Время подтвердило идеи русского ученого. Проникновению математики в квантовую физику, химию, биологию предшествовала разработка прерывной – дискретной – математики, которая, кроме теории чисел, сегодня включает в себя матричное исчисление, комбинаторную геометрию, теорию конечных автоматов и др. Но как бы причудливы и разнообразны ни были разделы дискретной математики, они вытекают из того же фундаментального требования, на котором зиждется и теория непрерывных функций – математический анализ.
        Требование это – однозначность.
        «В настоящее время, - пишет советский математик В. Тростников, - в математике не принято говорить о многозначных функциях; функцией, по определению, называется сопоставление каждому значению аргумента единственного значения функции». А при таком подходе на сферы приложения математики выпадают многие процессы окружающего нас мира, в частности, процессы перехода веществ из одного агрегатного состояния в другое, пороговые эффекты в биологии и т.д. Вот почему весьма злободневно звучат сегодня мысли Бугаева о функциях, обратных прерывным. Он называет их функциями произвольных величин, так как они могут иметь бесчисленное множество значений для одного и того же значения независимой переменой. В качестве примера Бугаев приводил известный закон Вебера, согласно которому ощущение и раздражение связываются между собой логарифмической функцией. Однако при этом обнаруживается интересная особенность. В то время как раздражение изменяется непрерывно, ощущение изменяется скачками. Чтобы, скажем, рукой ощутить увеличение положенного на нее груза, надо его вес увеличить не менее чем на одну треть первоначальной величины. Это  значит, что ощущение есть прерывная функция впечатления. И обратно: впечатление как функция данного ощущения есть произвольная величина, способная получить любое значение в определенных границах изменения. Таким образом, в данном индивидууме данному впечатлению всегда соответствует определенное ощущение, но данному ощущению может соответствовать множество впечатлений. Отсюда с неизбежностью следовал вывод: к области психики неприложим закон механического детерминизма, психическая причинность немыслима без элемента произвольности. «Некоторая доля случайности, появляющаяся в наших действиях, вносит элемент случайности в самую природу. Таким образом, случайность выступает на сцену как присущее свойство некоторых мировых явлений. В мире господствует не одна достоверность».
        К сожалению, Бугаев не смог предложить никакого математического аппарата, с помощью которого можно было бы исследовать безграничное множество открывшихся перед ним объектов. Думается, всеобщий интерес к работам Рене Тома объясняется тем, что его теорию катастроф можно считать первой удачной попыткой такого рода. Хотя эта теория и приложима к катастрофическому разрушению мостовых ферм и опор, область ее применения гораздо шире, чем можно предположить по названию. Это и возбуждение нервного волокна, и переход ламинарного течения в турбулентное, и внезапная потеря человеком самообладания, и превращение жидкости в пар, и деление клетки, и крах биржи и т.д.
        Такая широкая сфера применения поначалу даже породила стремление рассматривать весь окружающий нас мир как арену действия таких непрерывно происходящих «катастроф». Но, думается, в таком расширении понятия «катастрофа» нет нужды. Правильнее считать, что Тому удалось изобрести математический образ, позволяющий смоделировать скачкообразный переход количества в качество. Образ, позволяющий показать, как непрерывно меняющиеся причины приводят к резким, прерывно меняющимся следствиям, как ничтожное изменение начального состояния может привести к мгновенному, заранее непредсказуемому результату. При таком толковании «катастрофой» могут быть названы многие процессы, далеко не всегда несущие какую-либо угрозу или убыток человечеству. В этом можно убедиться, изучая придуманную английским математиком Э.Зееманом «машину катастроф».
        Нет, нет! Никаких разрушительных действий эта машина не производит. Она состоит (см. рис.1) из диска, вращающегося вокруг вертикальной оси. К одной из точек на периферии диска прикреплены две резиновые нити. Свободный конец одной из нитей жестко закреплен в точке Q, а свободный конец другой – Р – может свободно перемещаться в плоскости, параллельной плоскости диска. Опыт показывает, что, когда Р попадает в любую точку, находящуюся вне ромбовидной области АВСД, у диска есть только одно положение устойчивого равновесия. Когда же Р попадает внутрь этой области, устойчивых положений два.
        Как же это отражается на поведении диска? Если Р плавно перемещать вне ромбовидной области, диск будет плавно поворачиваться в ту или в другую сторону. Но когда Р попадает в область АВСД, положение меняется. Предположим, точка Р движется по линии UVWXYZ слева направо. При медленном движении точки диск плавно поворачивается. Но вот когда Р выходит из ромба в точке Y, диск резко, скачком меняет угол поворота. Но самое удивительное: когда Р начинает перемещаться в обратном направлении по той же прямой, в точке Y никакого скачка не происходит. Он появляется на этот раз в точке V, там, где Р выходит из ромба. Таким образом, поведение диска не меняется на прямо противоположное, когда Р проходит прежний путь ZYXWVU в обратном направлении.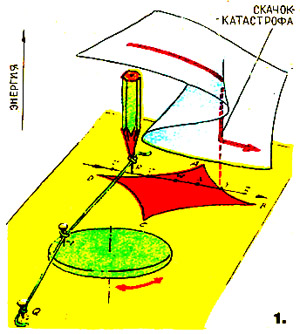


   























        Будучи специалистом в области топологии, Том предложил образ, с помощью которого можно описывать поведение «машины катастроф». Это трехмерное пространство, в котором по вертикальной оси откладывается энергия равновесных положений диска Х, а по горизонтальным осям – координаты точки Р. Основа образа – поверхность со складкой, изображающая собой совокупность всех равновесных положений диска. Проекция складки на плоскость образует часть ромбовидной области, примыкающей к точке А. Когда Р находится вне заштрихованной области, каждому ее положению соответствует одно-единственное значение Х и одна-единственная точка на поверхности: состояние системы здесь описывается однозначной функцией. Но когда Р оказывается внутри заштрихованной площади, одному положению Р соответствуют три значения Х на разных частях складки. Функция здесь перестает быть однозначной.
        Такая модель хорошо объясняет поведение диска. При движении Р слева направо Х движется вдоль гладкой поверхности до тех пор, пока не достигается край перегиба. Дальнейшее нарастание координаты приводит к резкому перескоку Х с верхнего на нижний уровень – так называемая «катастрофа» Тома. При движении Р в обратном направлении – справа налево – Х перемещается плавно по нижней поверхности складки, пока не достигнет ее края. Дальнейшее изменение координаты приводит снова к «катастрофе» – скачку с нижнего на верхний уровень.
        Эта простейшая модель, в которой энергия равновесия зависит всего от двух независимых переменных – координат точки Р. Том исследовал более общий случай: системы, поведение которых при изменении конечного набора независимых переменных а, в, с... зависит от конечного набора параметров х, у..., а энергия равновесия также зависит как от этих параметров, так и от независимых переменных а, в, с... Считая, что для реальных систем количество независимых переменных должно быть не более четырех – три пространственных координаты и одна временная, - Том доказал теорему: за немногими исключениями, не представляющими интереса, всегда возможно такое плавное и обратимое изменение независимых переменных, при котором в окрестностях данной точки система в зависимости от вида энергетической функции претерпит одну из семи «элементарных катастроф». Название каждой из них определяется видом поверхности энергии равновесия: перегиб, пик, ласточкин хвост, бабочка, гиперболический, эллиптический и параболический узлы.
        Такова вкратце теоретическая суть. Но есть уже и кое-какие практические приложения идей Рене Тома.
        Одна из первых попыток применения теории катастроф была сделана для описания разбивающихся о преграду волн. Как недавно выяснилось, попытка эта оказалась некорректной, поскольку давала неправильное описание процесса после того, как волна утрачивала свою форму. Эта неудача должна служить напоминанием о том, что не всякий разрушительный процесс может считаться «катастрофой Тома». Наоборот, процесс, не сопровождающийся какими-либо разрушениями, нередко оказывается именно такой «катастрофой».
        Например, в гидродинамике идеальных, лишенных вязкости жидкостей есть функция, в которой нетрудно узнать «энергетическую функцию» теории катастроф. Это дает возможность применить теорию для изучения, скажем, двухмерного потока, создаваемого шестью симметрично расположенными, вращающимися навстречу друг другу роликами (рис.2). Линии тока получаются такими, какие показаны на рисунке слева только в том случае, если скорость вращения всех роликов одинакова. Малейшее отклонение в скоростях вращения приводит к «катастрофе» – скачкообразному изменению картины линий тока. Так, если все ролики, вращающиеся против часовой стрелки, увеличат свою скорость, картина мгновенно перестроится и станет такой, как показано на рисунке справа.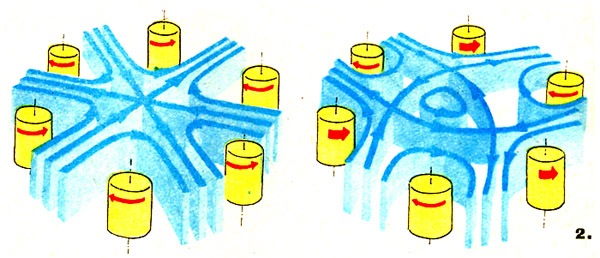







 













        С помощью теории катастроф можно быстро, не строя самих картин, предсказать, что  в общей  сложности могут существовать всего лишь 10 типов таких картин, и не больше.
        Другое практическое применение было сделано Зееманом, попытавшимся объяснить результаты исследований немецкого психолога К.Лоренца. Изучая реакции собак, Лоренц обнаружил, что, когда собака доведена до высокого уровня страха и злобы одновременно, ее поведение становится непредсказуемым: она может начать кусаться или бежать без каких-либо видимых признаков, по которым можно было бы судить об ее поведении в следующий момент. Более того, при одних и тех же значениях показателей страха и ярости животное могло повести себя совершенно по-разному.
        Зееман предположил, что такое поведение хорошо описывается «пиковой катастрофой» Тома. Эта модель разъяснена уже достаточно хорошо, чтобы читатели сами смогли разобраться в приведенной схеме (рис.3) и понять, какое есть глубокое качественное различие между поведением животного в состоянии спокойствия и возбуждения. По этой модели можно даже предсказать и проверить экспериментально существование расхождения в поведении собаки в том случае, когда страх и ярость возбуждаются одновременно. Действительно, в этом случае поведение собаки может «пойти» по верхней – агрессивной – или по нижней – «трусливой» – частям катастрофической складки, и ее поведение будет полностью определяться с самого начала сделанным «выбором». Из анализа этой модели нетрудно сделать еще один вывод: возбужденное животное скорее склонно броситься кусаться или обратиться в бегство, нежели пребывать в состоянии пассивной нейтральности.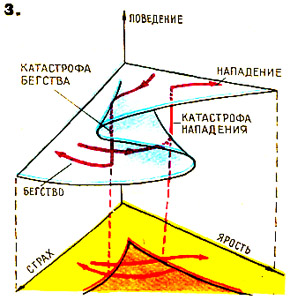



       




















        Увлекшись логичностью этих построений, Зееман предложил еще одно – весьма, конечно, спорное – применение теории катастроф: объяснение событий, происходящих во время знакомства юноши и девушки. На приведенной схеме (рис.4) ясно видно, что в начале знакомства у Него инициатива к сближению сильна, а у Нее, напротив, наблюдается легкая тенденция к отчуждению. Затем, когда, удрученный неуспехом, Он прекращает свои попытки, у Нее стремление к сближению становится очень сильным, и их взаимные отношения быстро несутся к перегибу складки. И если здесь Он сделает попятный шаг, отношения гораздо раньше, чем если бы они были предоставлены естественному ходу событий, могут мгновенно достичь состояния, которое все мы именуем взаимным увлечением, а Том - «катастрофой»...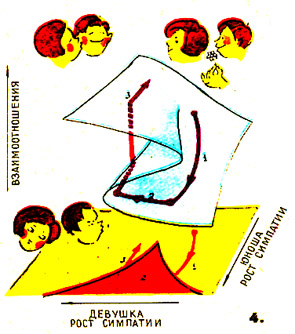



       






















        Этот пример, показывающий, до каких пределов может дойти увлечение модной математической теорией, свидетельствует в то же время о том, как нуждаются сейчас естественные науки в новых математических образах и математических аппаратах. Даже в таких хорошо разработанных отраслях, как сопротивление материалов, строительная механика, гидро- и аэромеханика, оптика, теория катастроф дала новые, нетривиальные результаты и подходы. Сам Том считает более важной сферой применения своих исследований биологию, прежде всего эмбриологию, где уже сделаны первые попытки создать математическую модель развития зародыша. Некоторые социологи и экономисты на Западе уповают на то, что теория катастроф даст в их руки ключ для объяснения механизма финансовых и экономических кризисов и банкротств.
        Думается, такое расширенное толкование чисто математических закономерностей есть результат недостаточно критического подхода к ним. Безупречная с точки зрения чистой математики, теория катастроф может дать надежные результаты в естественных науках лишь тогда, когда будут тщательно осознаны и проанализированы допущения, с помощью которых она стыкуется с процессами реального мира.
        А влияние этих допущений даже в таких науках, как физика и химия, осознано еще так мало, что американский физик Е.Вигнер прямо называл эффективность математики в естественных науках «непостижимой».
        Подвигнутый на свои исследования мыслью о том, что «история Вселенной есть неустанное созидание, развитие и разрушение форм» и что «цель науки провидеть эти изменения форм и, если можно, объяснить их», сам Рене Том прекрасно понимает, чего можно, а чего нельзя ожидать от разработанной им теории. «Ни в коем случае, - говорит он, - математик не может диктовать что-либо природе. Познавательная ценность теории катастроф в естественных науках сомнительна, если не считать физики и химии, где возможно создание точных моделей. Все остальные утверждения делаются на чисто качественно уровне...»

Справка:

Смирнов Герман Владимирович, более 30 лет вел в журнале «Техника - молодежи» рубрику «Клуб ТМ» - курьезные и смешные истории о знаменитых ученых и инженерах, причуды изобретательства, парадоксальные случайности, немыслимые совпадения, малоизвестные обстоятельства общеизвестных открытий, приключения идей, происхождение научных терминов и символов.
Смирнов Г.В., «Досье эрудита», М.: ЗАО МК-периодика, 2001. 256 стр.

Бугаев Николай Васильевич (1837-1903), русский математик. Отец писателя Андрея Белого. Окончил Московский университет (1859). С 1866 профессор этого же университета, член-корреспондент Петербургской АН (1897). Н.В. Бугаев - один из создателей Московского математического общества (президент с 1891) и его органа – «Математический сборник». Большая часть Н.В. Бугаева многочисленных математических работ относится к анализу и теории чисел.

Том (Thorn) Рене Фредерик (1923 г.р.), французский математик и философ, профессор Университета Страсбурга, член Парижской Академии наук (1976). Основные направления научных интересов - алгебраическая топология, дифференциальная топология. Р.Том - создатель математической теории катастроф.